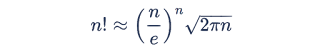In this presentation, I made reference to some dimensional weirdnesses. While making the point that additional dimensions make room for more stuff (as I put it), I pointed out that if you put four unit circles in the corners of a square of side 4, you have room for a central circle of radius r = 0.414. (Approximately. It's actually one less than the square root of 2.)
Correspondingly, if you put eight unit spheres in the corners of a cube of side 4, you have enough space for a central sphere of radius r = 0.732 (one less than the square root of 3), because the third dimension makes extra room for the central sphere.
If you were to put a sphere exactly in the middle of the front four spheres, or in the middle of the back four spheres, it would have a radius of r = 0.414, just as in two dimensions, but by pushing it in between those two layers of spheres, we make room for a larger sphere.
Finally (and rather more awkwardly, visually speaking), applying the same principle in four dimensions makes room for a central hypersphere of radius r = 1 (one less than the square root of 4).
The situation for general dimension d (which you've probably guessed by now) can be worked out as follows. Consider any pair of diametrically opposed unit hyperspheres within the hypercube (drawn in orange below). Those two hyperspheres are both tangent to the central green hypersphere, and they are also tangent to the sides of the blue hypercube.
We can figure out the distances from the center of any unit hypersphere to its corner of the hypercube, as well as to the central hypersphere. Since we also know the distance between opposite corners of the hypercube, we can obtain the radius of the central hypersphere:
One other oddity had to do with the absolute hypervolume, or measure, of unit hyperspheres in dimension d. A one-dimensional "hypersphere" of radius 1 is just a line segment with length 2. In two dimensions, a circle of radius 1 has area π = 3.14159; in three dimensions, the unit sphere has volume 4π/3 = 4.18879.... The measure of a unit hypersphere in dimension d is given by
For odd dimensions, this requires us to take a fractional factorial, which we can do by making use of the gamma function, and knowing that
With that in mind (and also knowing that n! = n (n – 1)! for all n), we can complete the following table for hyperspace measures:
That last entry may come as a bit of a surprise, but it is simply a consequence of the fact that as a number n grows without bound, πn grows at a constant pace (logarithmically speaking), while n! grows at an ever increasing rate. As a result, the denominator of Vd totally outstrips its numerator, and its value goes to zero.
But what if we combine the two, and ask how the measure of the central green hypersphere, expressed as a proportion of the measure of the blue hypercube, evolves as the number of dimensions goes up? On the one hand, we've seen that the measure of a unit hypersphere goes to 0 as the number of dimensions increases, but on the other hand, the central green hypersphere isn't a unit hypersphere; rather, its radius goes up roughly as the square root of the number of dimensions. How do these two trends interact with increasing dimensionality? In case it helps your intuition, here's a table for the ratios for small values of d.
Those of you who want to work it out for yourself may wish to stop reading here for the moment. Steven Landsburg, who is a professor of economics at the University of Rochester but earned his Ph.D. in mathematics at the University of Chicago, told a story of attending a K-theory conference in the early 1980s, in which attendees were asked this very question. Actually, they were specifically asked not to calculate the limiting ratio, but rather to guess what it might be, from the following choices:
- –1
- 0
- 1/2
- 1
- 10
- infinity
Attendees were invited to choose three of the six answers, and place a bet on whether the correct answer was among those three. Apparently, most of the K-theorists reasoned as follows: Obviously, the measure can't be negative, so –1 can safely be eliminated. Then, too, the central green hypersphere "obviously" fits within the blue hypercube, so its volume can't be greater than that of the hypercube, so the ratio of the two can't be greater than 1, so 10 and infinity can likewise safely be eliminated.
Well, "obviously," you know that the hypersphere can in fact go outside the hypercube, so 10 and infty can't actually be eliminated. So what is the right answer?
At the risk of giving the game away so soon after offering it, I'll mention that the answer hinges on, of all things, whether the product of π and e is greater or less than 8. Here's how that comes about: We know that the measure of a unit hypersphere in dimension d is given by
But that's just the unit hypersphere. If we take into account the fact that the radius of the central green hypersphere is
then the question becomes one of the evolution of the measure Gd of the central green hypersphere:
To figure out how this behaves as d goes to infinity, we first rewrite it as
Next, we make use of Stirling's approximation to the factorial function:
Applying this to n = d/2 gives us
and when expressing it as a proportion of the measure of the hypercube of side 4, we get
Finally, we observe that we can write (by taking into account one extra higher-order term in the usual limit for 1/e)
and we see that
The right-hand side is eventually dominated by the factor involving πe/8 = 1.06746..., which drives the ratio Gd/4d to infinity as d increases without bound—but it takes a long time. A more precise calculation shows that the fraction first exceeds 1 at dimension d = 1206. A plot of the ratio as a function of dimension looks like this:
Notice that the ratio reaches a minimum of very nearly 0.00001 at 264 dimensions; the exact value is something like 0.00001000428. As far as I know, that's just a coincidence.