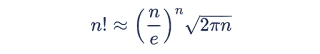High-Dimensional Weirdness

At work, I run a mathematics colloquium that meets every other Thursday.  I don't always present—I probably present about 20 to 25 percent of the time—but I did a recent one on the behavior of high-dimensional spaces.  I then came upon an oddity that I thought was worth sharing, for those three or four of you who might like that kind of thing.

In this presentation, I made reference to some dimensional weirdnesses.  While making the point that additional dimensions make room for more stuff (as I put it), I pointed out that if you put four unit circles in the corners of a square of side 4, you have room for a central circle of radius r = 0.414.  (Approximately.  It's actually one less than the square root of 2.)

 

Correspondingly, if you put eight unit spheres in the corners of a cube of side 4, you have enough space for a central sphere of radius r = 0.732 (one less than the square root of 3), because the third dimension makes extra room for the central sphere.

If you were to put a sphere exactly in the middle of the front four spheres, or in the middle of the back four spheres, it would have a radius of r = 0.414, just as in two dimensions, but by pushing it in between those two layers of spheres, we make room for a larger sphere.

Finally (and rather more awkwardly, visually speaking), applying the same principle in four dimensions makes room for a central hypersphere of radius r = 1 (one less than the square root of 4).

The situation for general dimension d (which you've probably guessed by now) can be worked out as follows.  Consider any pair of diametrically opposed unit hyperspheres within the hypercube (drawn in orange below).  Those two hyperspheres are both tangent to the central green hypersphere, and they are also tangent to the sides of the blue hypercube.

We can figure out the distances from the center of any unit hypersphere to its corner of the hypercube, as well as to the central hypersphere.  Since we also know the distance between opposite corners of the hypercube, we can obtain the radius of the central hypersphere:

One interesting consequence is that at dimension d = 4, the central green hypersphere is now as large as any of the orange unit hyperspheres, and above dimension d = 9, the central hypersphere is actually large enough to poke out of the faces of the hypercube.  Keep that in mind for what follows.



One other oddity had to do with the absolute hypervolume, or measure, of unit hyperspheres in dimension d.  A one-dimensional "hypersphere" of radius 1 is just a line segment with length 2.  In two dimensions, a circle of radius 1 has area π = 3.14159; in three dimensions, the unit sphere has volume 4π/3 = 4.18879....  The measure of a unit hypersphere in dimension d is given by

For odd dimensions, this requires us to take a fractional factorial, which we can do by making use of the gamma function, and knowing that

With that in mind (and also knowing that n! = n (n – 1)! for all n), we can complete the following table for hyperspace measures:

That last entry may come as a bit of a surprise, but it is simply a consequence of the fact that as a number n grows without bound, πⁿ grows at a constant pace (logarithmically speaking), while n! grows at an ever increasing rate.  As a result, the denominator of V_d totally outstrips its numerator, and its value goes to zero.



But what if we combine the two, and ask how the measure of the central green hypersphere, expressed as a proportion of the measure of the blue hypercube, evolves as the number of dimensions goes up?  On the one hand, we've seen that the measure of a unit hypersphere goes to 0 as the number of dimensions increases, but on the other hand, the central green hypersphere isn't a unit hypersphere; rather, its radius goes up roughly as the square root of the number of dimensions.  How do these two trends interact with increasing dimensionality?  In case it helps your intuition, here's a table for the ratios for small values of d.

Those of you who want to work it out for yourself may wish to stop reading here for the moment.  Steven Landsburg, who is a professor of economics at the University of Rochester but earned his Ph.D. in mathematics at the University of Chicago, told a story of attending a K-theory conference in the early 1980s, in which attendees were asked this very question.  Actually, they were specifically asked not to calculate the limiting ratio, but rather to guess what it might be, from the following choices:

• –1
• 0
• 1/2
• 1
• 10
• infinity

Attendees were invited to choose three of the six answers, and place a bet on whether the correct answer was among those three.  Apparently, most of the K-theorists reasoned as follows: Obviously, the measure can't be negative, so –1 can safely be eliminated.  Then, too, the central green hypersphere "obviously" fits within the blue hypercube, so its volume can't be greater than that of the hypercube, so the ratio of the two can't be greater than 1, so 10 and infinity can likewise safely be eliminated.

Well, "obviously," you know that the hypersphere can in fact go outside the hypercube, so 10 and infty can't actually be eliminated.  So what is the right answer?

At the risk of giving the game away so soon after offering it, I'll mention that the answer hinges on, of all things, whether the product of π and e is greater or less than 8.  Here's how that comes about: We know that the measure of a unit hypersphere in dimension d is given by

But that's just the unit hypersphere.  If we take into account the fact that the radius of the central green hypersphere is

then the question becomes one of the evolution of the measure G_d of the central green hypersphere:

To figure out how this behaves as d goes to infinity, we first rewrite it as

Next, we make use of Stirling's approximation to the factorial function:

Applying this to n = d/2 gives us

and when expressing it as a proportion of the measure of the hypercube of side 4, we get

Finally, we observe that we can write (by taking into account one extra higher-order term in the usual limit for 1/e)

and we see that

The right-hand side is eventually dominated by the factor involving πe/8 = 1.06746..., which drives the ratio G_d/4^d to infinity as d increases without bound—but it takes a long time.  A more precise calculation shows that the fraction first exceeds 1 at dimension d = 1206.  A plot of the ratio as a function of dimension looks like this:

Notice that the ratio reaches a minimum of very nearly 0.00001 at 264 dimensions; the exact value is something like 0.00001000428.  As far as I know, that's just a coincidence.

Cicada Recurrence and the Allee Effect

One of the best-known phenomena in the insect world is the unusual recurrence of various populations of cicada.  There aren't any cicadas out here on the West Coast, where I live, but they are endemic to the Northeast.  The periodical cicadas (there are non-periodical cicadas, apparently) are notorious for having life cycles that are synchronized to one of two (relatively) large primes: 13 years and 17 years.  The big question, of course, is why: Why do cicadas have life cycles that are synchronized in this fashion?

One could divide the 13-year cicadas into 13 distinct subgroups, depending on which year they emerged, and divide the 17-year cicadas into 17 subgroups along the same principle.  Physical observation of cicadas, as shown in the Wikipedia plot summary, reveals that only about half of the 13+17 = 30 subgroups actually manifest in the United States (where the cicada is native), however, with two subgroups becoming extinct within the last century or two.  Nonetheless, the periodicity is well enough established that there should be a rational explanation of this phenomenon.

 One historically proposed reason for the synchronization has been that the long recurrence time limits exposure of the species above ground to predators, and that when they are exposed, there are so many of them that predators cannot possibly decimate them (a fact well attested by the unfortunate farmers who have to deal with them), thereby ensuring the continued existence of the population.  Although this is surely part of the answer, it only explains why the period is long; it doesn't explain why the period isn't 12 or 15, for instance, rather than 13 or 17.  These latter periods would only provide additional benefit if the likely predators of the cicada likewise had a life cycle punctuated by years of inactivity, which turns out not to be so.

A more successful explanation involves hybridization.  It is hypothesized that whatever mechanism governs the return of the population after however many years is based on a biological clock that is adjusted to activate periodically, and that if a 13-year cicada were to mate with a 17-year cicada, the result would be a substantial number of cicadas with unpredictable, but likely shorter, periods.  (Too long, and the individuals would die of old age, anyway.)  Such offspring would be more vulnerable to predation, so there is an evolutionary premium placed against hybridization.  Computer simulation studies show, however, that if we assume an initial species-wide distribution of a variety of periods—some prime-numbered, some composite—the prime-numbered periods remain, but so do some of the composite periods.

This 2009 paper, by Tanaka et al., explains away the remaining composite periods by means of something called the Allee effect.  In many population dynamics analyses, it is assumed that the fewer instances of a species exist, the more likely any instance is to survive—it being presumed that there is no disadvantage owing to an excess of resources.  There may be no such disadvantage, but it is nonetheless the case that there are situations where the reverse is true, for small populations: the greater the population, the more likely any individual is to survive to reproduce, because it benefits from the increased support and robustness of the larger population, up until the point where that larger population represents more competition than cooperation.  This reverse but very natural-seeming tendency constitutes the Allee effect.

Tanaka and company simulated the cicada species under a very simple hybridization model, both with and without the Allee effect, starting with subgroups with a range of periods varying from 10 through 20 years.  They found that without the Allee effect, there was broad survival of all of the cicada subgroups, with the 16-year subgroup thriving the best.  But with the Allee effect, the result was startlingly different: Only those cicada subgroups with periods of 13, 17, or 19 years survived, depending on some of the initial parameters.

Since the actual mechanism of the periodicity is not well understood yet, this study is more suggestive than dispositive, but the results are provocative.

Competing at the Limit

I participate from time to time at a site called Math StackExchange, where users ask and answer questions about mathematics.  Most often, the questions relate to a student's coursework, but there are some deeper questions as well.  It's one of a family of similar StackExchange sites devoted to a wide variety of topics, only some of which are academically inclined.

One question that comes up every now and then is the definition of a limit.  It looks like this:

limx→af(x)=L⇔∀ε>0,∃δ>0,∀x,0<|x−a|<δ⇒|f(x)−L|<ε

And it reads like this:

The limit of f(x) as x approaches a equals L, if and only if for every positive ε, there exists a positive δ such that whenever x is within δ of a (except possibly exactly at a), f(x) is within ε of L.

Understandably, to many math students starting introductory analysis, this looks like so much gobbledygook.  Textbooks typically try to aid understanding by drawing a picture of a function f(x) in the vicinity of some value x = a, showing that as x gets closer to a, f(x) in turn gets closer to its limiting value L (which might not in fact be f(a) itself, if that value even exists).

But what if the sticking point for students isn't always that notion of better and better approximations (central as that is to the definition of a limit)?  What if the sticking point is the interplay between the "for every" (symbolized by the upside-down A: ∀) and the "there exists" (symbolized by the upside-down E: ∃)?  The intent of this definition, first conceived of by the French mathematician Augustin-Louis Cauchy (1789–1857) and formalized by the Bohemian mathematician/philosopher Bernard Bolzano (1781–1848), is to ensure that we can always get as close as we want to the limiting value (without necessarily hitting it), simply by being as close as we need to be to the argument x = a.

We can represent this as a sort of (almost irredeemably nerdy) game between two players, the Verifier and the Falsifier.  The Verifier is trying to prove the limit is right by showing that everything near x = a maps to an f(x) that's close to L, while the Falsifier tries to disprove the limit by challenging the Verifier to get even closer to L.  For instance, if the function f(x) = 2x+3, the Verifier might be trying to demonstrate that the limit of f(x), as x approaches 5, is 13:

Falsifier.  I don't think it's true; I think the limit is not 13.

Verifier.  Well, if that's so, then you must think there's some neighborhood of 13 that I can't force f(x) to lie in.

Falsifier.  Right.  OK, I challenge you to get within 0.1 of 13.

Verifier.  Sure.  If x is within 0.05 of 5, then f(x) will be within 0.1 of 13: f(4.95) = 2×4.95+3 = 12.9, which is within 0.1 of 13, and f(5.05) = 2×5.05+3 = 13.1, which is also within 0.1 of 13.  [There is more to it than that, such as that f(x) is monotonically increasing, but we'll leave these details out for now.]

Falsifier.  All right, but can you get within 0.01 of 13?

Verifier.  Yes.  All I have to do is force x to be within 0.005 of 5: f(4.995) = 12.99 and f(5.005) = 13.01.  In fact, I can answer any neighborhood of 13 you challenge me with, simply by halving it to obtain my vicinity of x = 5.  If you want me to be within ε of 13, then all I have to do is be within δ = ε/2 of 5.  Then f(5–ε/2) = 2×(5–ε/2)+3 = 13–ε, and f(5+ε/2) = 2×(5+ε/2)+3 = 13+ε.  It's foolproof.

Falsifier.  Hmm, I guess you're right.  I'll have to concede that the limit is 13.

The exchange would have gone quite differently if Verifier had claimed that the limit was 12.  Then, for instance, when Falsifier challenged Verifier to get within, say, 0.1 of 12, Verifier would have been unable to choose a vicinity of x = 5 such that f(x) is between 11.9 and 12.1 over that entire vicinity, because any value of x very close to 5—close as we like—always has f(x) very close to 13, and that clearly doesn't fall between 11.9 and 12.1.  But if Verifier can always figure out the right vicinity to force the function to fall in Falsifier's neighborhood, then they can prove the limit to be correct.

This approach to proofs has much broader applicability; in game semantics, and in a kind of logic called independence-friendly logic, many demonstrations rely on this kind of interplay between a Falsifying universal quantifier (the "for every" ∀) and an existential quantifier (the "there exists" ∃).

---

Now for a digression to something that will seem totally unrelated at first.

In the late 11th century, into the 12th, there lived a Breton named Pierre le Pallet who was a precocious philosopher.  He was initially trained by William of Champeaux, but quickly grew capable of duelling wits with his teacher, and ended by starting a school of his own, against the advice of William.  By all accounts, he was a self-proud man, convinced simultaneously that he was brighter than anyone else and that no one else was giving him proper credit for this.  In his defense, he was generally regarded as one of the leading philosophers of his time, his specialty being logic, a tool that he wielded in an almost competitive spirit in defense of positions that were then considered heretical.  It was during his late adolescence that he took on the name that we know him by today, Peter Abelard.

As Abelard, his fame grew considerably, and people from all around sought his counsel.  One of these was a canon in Notre Dame named Fulbert, who wanted Abelard as a tutor for his niece.  She was then in her early twenties (we think—there is significant uncertainty about her birthdate), and had demonstrated herself to be remarkably capable in classical letters.  She had mastered Latin, and Greek, and Hebrew, and had applied these to a study of Christianity, to which she was devoutly dedicated.

Her name was Heloise d'Argenteuil, and she and her relationship with Abelard were in time to become famous.  Both of them found the other attractive, and in or around 1115, they started an affair just out of the watchful eye of her uncle.  Ostensibly, Abelard was tutoring her, but this would be interrupted periodically by a bout of lovemaking.  When they were separated, they would exchange personal messages on wax slate (parchment being too expensive even for billet doux that would have to be discarded or hidden).  A message would be incised on a layer of wax mounted to a wooden back; this message could then be read and the wax melted and smoothed over to be used again and again.

The two lovers could not necessarily deliver the messages personally without incurring Fulbert's suspicion, and so would have to rely on the discretion of messengers.  But as the messages were typically written in Latin or Greek, which the messengers couldn't read, teacher and pupil could exchange their letters under the apparent guise of lessons.  Abelard and Heloise apparently exchanged over a hundred letters this way, letters we have access to only because Heloise seems to have transcribed them onto a scroll (now lost) which was found centuries later by a French monk named Johannes de Vepria.

The affair progressed as far as Heloise bearing a son by Abelard, whom she called Astrolabe, after the astronomical instrument, and about whom we know almost nothing at all.  Around this time, Fulbert caught wind of it, and managed to force them to marry, although Abelard extracted a promise from Fulbert not to publicize the marriage, so as to protect Abelard's reputation.

Fulbert, however, had had his own reputation damaged by Abelard over other matters, and so he began spreading rumors of the marriage.  Abelard had Heloise installed at an abbey for her own protection, a gesture that Fulbert misunderstood as Abelard trying to wash his hands of her.  So Fulbert hired some henchmen, and one night, they went to Abelard's sleeping quarters, and castrated him.

---

Abelard went into seclusion, and it is unclear that he ever saw Heloise again after this time.  However, about a decade or two later, they exchanged a sequence of seven or so longer letters, instigated when Heloise somehow got her hands on a letter that Abelard had written to a monk about his life story.  That letter included a retelling of her own story, and the two lovers were reintroduced to one another in this way.

Except that by this time, Abelard had decided to impose a sort of pious asceticism on himself that extended to any romantic feelings he might have had for his one-time wife.  Heloise, in turn, wrote him back, entreating him to concede those feelings, feelings she was sure he still retained.  In the last pair of letters, Heloise appears to have relented, and buried herself in her religious life, and Abelard seems to have praised and encouraged this.  But these letters are permeated through and through with an almost overwrought subtext.

So who convinced whom?  As if in honor of these two, whose story has become synonymous with medieval romance, the roles of the Falsifier and the Verifier are often personified by the love-denying Abelard, whose initial is a convenient mnemonic for the universal quantifier ∀, and by the love-asserting Heloise, whose name is sometimes spelled Eloise, whereby her initial is a convenient mnemonic for the existential quantifier ∃—symbols ineluctably entwined in the cherished logic of Abelard's youth.

The Most Beautiful Equation in Mathematics

What follows is a bit I did over at Math StackExchange.  Posting it over here was an experiment in whether the mathematical typesetting would transfer correctly in a copy-and-paste.  For the most part, as long as I leave it alone, it seems to have done so (modulo the line breaks being lost in the shuffle).

Euler's equation

eiπ+1=0

is considered by many to be the most beautiful equation in mathematics—rightly, in my opinion. However, despite what Gauss might say, it's not the most obvious thing in the world, so let's perhaps try to sneak up on it, rather than land right on it with a bang.

It's possible to think of complex numbers simply as combinations of real values and imaginary values (that is, square roots of negative numbers). However, plotting them on the complex plane provides a kind of geometric intuition that can be valuable.

On the complex plane, a complex number a+bi is plotted at the point (a,b). Adding complex numbers is then just like adding vectors—(a+bi)+(c+di)=(a+c)+(b+d)i, for instance—just as you might have expected. (It's probably useful to draw some of these out on graph paper, if you can.)

Multiplication is where things get a little unusual. Multiplication by real values is just as you'd expect, generalizing from the one-dimensional real number line to the two-dimensional complex plane: Just as k times a positive number is (for positive k) another positive number k times as far from the origin, and correspondingly for negative numbers, k times a complex number is another complex number, k times as far from the origin, and in the same direction.

But multiplication by imaginary values is different. When you multiply something by i, you don't scale that something, you rotate it counter-clockwise, by 90 degrees. Thus, the number 5, which is 5 steps to the east (so to speak) of the origin, when multiplied by i becomes 5i, which is 5 steps to the north of the origin; and 3+4i, which is to the northeast, becomes −4+3i, which is to the northwest. And so on.

---

OK, let's step away from the complex plane for a moment, and proceed to the exponential function. We're going to start with the ordinary ol' real-valued exponential function, y=ex. There are lots of exponential functions: 2x,10x,πx,… But there's something special about the exponential function with e, Euler's constant, as its base.

If you graph y=ex, you get a curve that starts out at the far left, at (−∞,0) (so to speak), and proceeds rightward, crawling very slowly upward, so slowly that by the time it gets to x=0, it's gotten no further upward than (0,1). After that, however, it picks up speed, so that further points are (1,e),(2,e2),(3,e3),…, and by the time x=20, we've nearly halfway to a billion.

Another way to put that is that the derivative of y=ex, which you might think of as its slope, starts out as an almost vanishingly small number far to the left of the origin, but becomes very large when we get to the right of the origin.

To be sure, all exponential functions do that basic thing. However, the very unusual thing about y=ex is that its derivative—its slope, in other words—is exactly itself. Other exponential functions have derivatives that are itself multiplied by some constant. But only the exponential function, with e as its base, has a derivative that is exactly equal to itself.

It's very rare that an expression has that property. The function y=x2, for instance, has derivative (or slope) y′=2x, which is not equal to x2. But if you want to know the slope of y=ex at any point, you just figure out what y is, and there's your slope. At x=1, for instance, y=e≐2.71828, so the slope there is also y′=e≐2.71828.

The only functions that have that property have the form y=Cex, where C is any constant.

There's another way to think of the derivative that is not the slope, although it's related. It has to do with the effect that incremental changes in x have on y. As we saw above, the derivative of y=ex, at x=1, is also y′=ex=e≐2.71828.

That means that if you make a small change in x, from 1 to 1+0.001=1.001, then y approximately makes 2.71828 times as much of a change, from 2.71828 to 2.71828+0.00271828≐2.72100. This is only accurate for small changes, the smaller the better, and in this case at least is exact only in the limit, as the change approaches zero. That is, in fact, the definition of the derivative.

---

Now, let's return to the complex plane, and put the whole thing together. Let's start with e0=1. We can plot that point on the complex plane, and it will be at the point with coordinates (1,0). It's important to remember that this does not mean that 0=e1. The value of x is not being plotted here; all we're doing is plotting y=e0=1=1+0i, and that 1 and 0 are the coordinates of (1,0), which is one step east of the origin. By the unusual property of ex, the derivative is also 1.

Suppose we then consider making a small change to x=0. If we add 0.001 to x, we make a change to ex that is equal to the derivative times the small change in x. That is to say, we add the derivative 1 times the small change, 0.001, or just 0.001 again. So the new value would be close to (though not quite exactly) 1.001, which is represented by the point (1.001,0). It would be in the same direction from the origin—east—as the original point, but 0.001 further away.

But what happens if we add not 0.001 to x, but 0.001i? The derivative is still 1, so the incremental impact on ex is the derivative ex=1 times 0.001i, or 0.001i again. So the new value would be close to (though, again, not quite exactly) 1+0.001i, which is represented by the point (1,0.001). It would be 0.001 steps to the north of (1,0), because the extra factor of i rotates the increment counter-clockwise by 90 degrees.

Symbolically, we would say

e0.001i≐1+0.001i

Now, suppose we added another 0.001i to the exponent, so that we are now evaluating e0.002i. We'll do what we did before, which was to multiply the increment in the exponent, 0.001i, by the derivative. And what is the derivative? Is it 1, as it was before? No, since we're making an incremental step from e0.001i, it should be the derivative at 0.001i, which is equal to e0.001i again, which we determined above to be about 1+0.001i. If we multiply this new derivative value by the increment 0.001i, we get an incremental impact on ex of −0.000001+0.001i, which is a tiny step that is mostly northward, but which is also just an almost infinitesimal bit to the west (that's the −0.000001 bit). We've veered ever so slightly to the left, so the new estimated value at x=0.002i is

e0.002i≐0.999999+0.002i

One thing to observe about the small steps that we've taken is that each one is at right angles to where we are from the origin. When we were directly east of the origin, our small step was directly northward. When we were just a tiny bit north of east from the origin, our small step was mostly northward, but a tiny bit westward, too.

What curve could we put around the origin, such that if we traced its path, the direction we're moving would always be at right angles to our direction from the origin? That curve is, as you might have guessed already, a circle. And since we start off 1 step east of the origin, the circle has radius 1. Unsurprisingly, this circle is called the unit circle.

If we follow this line of reasoning, then the value of eiπ must be somewhere along this unit circle; that is, if eiπ=m+ni, then m2+n2=1 (since that's the equation of a circle of radius 1, centered at the origin). The only reason our estimated values weren't exactly on the unit circle is that we made steps of positive size, whereas the derivative is technically good only for steps of infinitesimal size. But where on the unit circle is eiπ?

The crucial observation is in how fast we make our way around the circle. When we made our first step, from x=0 to 0.001i, that step had a size, a magnitude, of 0.001, and the incremental impact on ex was also of magnitude 0.001. Our second step, from x=0.001i to 0.002i, was also of magnitude 0.001, and the incremental impact on ex was, again, about 0.001.

In order to get to eiπ, we would have to make a bunch of steps, whose combined magnitude total π. The result would be, if we reason as we did above, to move a distance π around the unit circle. Since the unit circle has radius 1, and diameter 2, its circumference must be 2π. Therefore, eiπ must be halfway around the circle, at coordinates (−1,0). That is none other than the complex value −1+0i=−1:

eiπ=−1

or, in its more common form,

eiπ+1=0

The foregoing is not, by any means, a rigorous demonstration. It's an attempt to give some kind of intuition behind the mysterious-looking formula.